Question

En un puesto de frutas deben decidir cuánto cobrar por sus productos. Deciden cobrar $5.30 por 1 manzana y 1

naranja. También planean cobrar $14 por 2 manzanas y 2 naranjas. Ponemos esta información en un sistema de
ecuaciones lineales.
¿Podemos determinar el precio único de una manzana y de una naranja?​

Answer 1

Este sistema de ecuación no tiene solución, puesto que lleva a un absurdo explicado en que los coeficientes dependientes de la segunda ecuación son múltiplos de los coeficientes dependientes de la primera y los coeficientes independientes son distintos.

Step-by-step explanation:

En este caso, el coste total es igual a la suma de los productos de coste unitario y cantidad de artículos comprados. Tenemos conocimiento de dos costes asociados a dos distintas combinaciones de dos productos, lo cual lleva a un sistema de dos ecuaciones lineales con dos incógnitas. En consencuencia, existe una solución única.

A continuación, presentamos las dos ecuaciones lineales en cuestión:

i) Deciden cobrar $ 5.30 por una manzana y una naranja

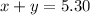`x+y = 5.30` (Ec. 1)

ii) También planea cobrar $ 14 por dos manzanas y dos naranjas

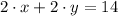`2\cdot x + 2\cdot y = 14` (Ec. 2)

Donde
`x`,
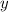`y` son los costes unitarios de las manzanas y las naranjas, medidas en pesos por unidad.

A continuación, procedemos a resolver este sistema:

Despejamos
`x` en (Ec. 1):

`x = 5.30-y`

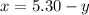
Y lo aplicamos en (Ec. 2):

`2\cdot (5.30-y)+2\cdot y = 14`

`10.60-2\cdot y+2\cdot y = 14`

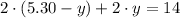
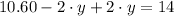
`10.60 = 14` (ABSURDO)

Este sistema de ecuación no tiene solución, puesto que lleva a un absurdo explicado en que los coeficientes dependientes de la segunda ecuación son múltiplos de los coeficientes dependientes de la primera y los coeficientes independientes son distintos.