Question

The graph of line BC is shown. Create an equation for a line perpendicular to line BC that passes through point A.

Answer 1

y = 3x + 1

Explanation:

Coordinates of the points given on line BC,

A(0, 1), B(-3, 2) and C(3, 0)

Since, slope of a line passing through two points
`(x_1,y_1)` and
`(x_2,y_2)` is,

m =
`(y_2-y_1)/(x_2-x_1)`

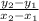
Therefore, slope of line BC,

`m_1=(2-0)/(-3-3)`

`=-(1)/(3)`

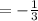
Let the slope of a line perpendicular to BC =
`m_2`

By the property of perpendicular lines,

`m_1* m_2=-1`

`(-(1)/(3))\tims m_2=-1`

`m_2=3`

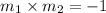
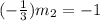
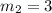
Since, equation of a line passing through point
`(x_1,y_1)` and slope m is given by,

`y-y_1=m(x-x_1)`

Therefore, equation of a line passing through A(0, 1) and slope = 3,

y - 1 = 3(x -0)

y - 1 = 3x

y = 3x + 1

Equation of the perpendicular line on BC and passing through point A is,

y = 3x + 1