Question

Find k if (x+6) is a factor of the polynomial
f(x) = 2x4 + 9x3 – 17x2 + kx – 12k

Answer 1

The value of k is 2

Explanation:

The polynomial remainder theorem

The polynomial remainder theorem states that the remainder of the division of a polynomial f(x) by (x-r) is equal to f(r).

The function:

`f(x) = 2x^4 + 9x^3 - 17x^2 + kx -12k`

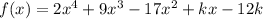
has a factor of (x+6).

Applying the polynomial remainder theorem for r=-6, substitute x=-6

`f(-6) = 2(-6)^4 + 9(-6)^3 - 17(-6)^2 + k(-6) - 12k`

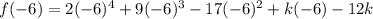
Operating:

`f(-6) = 2*1296 + 9*(-216) - 17*36 + k(-6) - 12k`

`f(-6) = 2592 - 1944 - 612 -6k - 12k`

`f(-6) = 36 -18k`

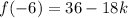
If x+6 is a factor, then the remainder is zero:

36 -18k=0

Subtracting 36:

-18k=-36

k=-36 / (-18)=2

k=2

The value of k is 2