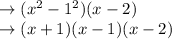Question

PLSSS ANSER FASTTTTTT

Answer 1

`{x}^(3) - {2x}^(2) - x + 2 \\ = {x}^(2) (x - 2) - 1(x - 2) \\ = ( {x}^(2) - 1)(x - 2) \\ = ( {(x)}^(2) - {(1)}^(2) )(x - 2) \\ = (x + 1)(x - 1)(x - 2)`

Answer:

(x + 1)(x - 1)(x - 2)

Hope you could understand.

If you have any query, feel free to ask.

Answer 2

`(x+1)(x-1)(x-2)`

Explanation:

`x^3-2x^2-x+2`

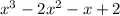
Look at this as 2 separate expressions for now, being the first 2 terms and the last 2 terms:

`\mbox{1. }x^3-2x^2\\\mbox{2. }-x+2`

Factor both of these individually, starting with the first one. The greatest common factor here is x², so factor that out:

`\rightarrow x^3-2x^2\\\rightarrow x^2(x-2)`

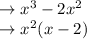
Now the second equation. There isn't really a GCF here, but you still should factor out a -1 to get the x on its own.

`\rightarrow -x+2\\\rightarrow -1(x-2)`

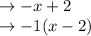
Together, that leaves you with this:

`x^2(x-2)-1(x-2)`

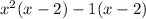
This is actually another expression that can be factored. The GCF here is (x - 2):

`\rightarrow x^2(x-2)-1(x-2)\\\rightarrow (x^2-1)(x-2)`

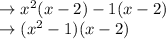
Finally, you can expand that (x² - 1) further using this rule:

`(x^2-y^2)=(x+y)(x-y)`

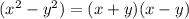
1 is equal to 1², so you can rewrite that term and then expand it with the rule above:

`\rightarrow (x^2-1^2)(x-2)\\\rightarrow (x+1)(x-1)(x-2)`