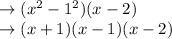Answer:

Explanation:
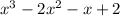
Look at this as 2 separate expressions for now, being the first 2 terms and the last 2 terms:
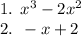
Factor both of these individually, starting with the first one. The greatest common factor here is x², so factor that out:
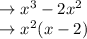
Now the second equation. There isn't really a GCF here, but you still should factor out a -1 to get the x on its own.
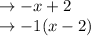
Together, that leaves you with this:
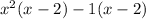
This is actually another expression that can be factored. The GCF here is (x - 2):
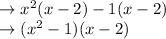
Finally, you can expand that (x² - 1) further using this rule:
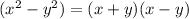
1 is equal to 1², so you can rewrite that term and then expand it with the rule above: