Question

Which of the following shows that △ABD≅△CBD, when y=5?

The figure shows quadrilateral A B C D with diagonal B D. The length of side A D is given by the formula 2 times y plus 5 units. The length of side C D is given by the formula y plus 10. The measure of angle A D B is given by the formula 2 times y plus 25 degrees. The measure of angle C D B is equal to 35 degrees.


∠ABD≅∠CBD, AB¯¯¯¯¯≅BC¯¯¯¯¯, and AD¯¯¯¯¯≅CD¯¯¯¯¯.So △ABD≅△CBD by SSS.


∠ABD≅∠CBD, BD¯¯¯¯¯≅BD¯¯¯¯¯, and AD¯¯¯¯¯≅CD¯¯¯¯¯.So △ABD≅△CBD by SAS.


∠ADB≅∠CDB, BD¯¯¯¯¯≅BD¯¯¯¯¯, and AD¯¯¯¯¯≅CD¯¯¯¯¯.So △ABD≅△CBD by SAS.


∠ADB≅∠CDB, AB¯¯¯¯¯≅BC¯¯¯¯¯, and AD¯¯¯¯¯≅CD¯¯¯¯¯.So △ABD≅△CBD by SSS.

Answer 1

The correct option is;

∠ADB ≅ ∠CDB,
`\overline {BD}` ≅
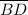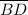`\overline {BD}` and
`\overline {AD}` ≅
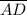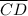`\overline {CD}`. So ΔABD ≅ ΔCDB by SAS

Explanation:

The given parameters are;

The polygon given = Quadrilateral

The diagonal of the quadrilateral = BD

The length of the side AD = (2×y + 5) units

The length of the side CD = (y + 10) units

The given measure of ∠ABD = (2 × y + 25)°

The given measure of ∠CBD = 35°

When y = 5, we have by substituting the value of y into the equations representing the dimensions of the quadrilateral ABCD;

The length of the side AD = 2 × y + 5 = 2×5 + 5 = 15 units

∴ The length of the side AD = 15 units

The length of the side CD = (y + 10) units = (5 + 10) units = 15 units

∴ The length of the side CD = 15 units

The measure of ∠ABD = (2 × y + 25)° = (2 × 5 + 25)° = 35°

The measure of ∠ABD = 35°

Therefore;

∠ADB ≅ ∠CDB by substitution

`\overline {BD}` ≅
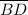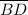`\overline {BD}` by reflexive property

`\overline {AD}` ≅
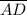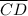`\overline {CD}` by substitution

∴ ΔABD ≅ ΔCBD by Side-Angle-Side rule of congruency