Question

In a two-digit number, the tens digit is 5 less than the units digit. The number itself is five more than three times the sum of its digits. What is the number?

Answer 1

38

Explanation:

Answer 2

Given:

In a two-digit number, the tens digit is 5 less than the units digit.

The number itself is five more than three times the sum of its digits.

To find:

The number.

Solution:

Let the two digit number is ab. So,

`ab=10a+b`

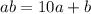
Tens digit is 5 less than the units digit.

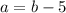`a=b-5` ...(i)

The number itself is five more than three times the sum of its digits.

`10a+b=3(a+b)+5`

`10a+b=3a+3b+5`

`10a+b-3a-3b=5`

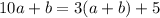
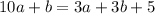
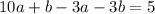
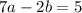`7a-2b=5` ...(ii)

Using (i) and (ii), we get

`7(b-5)-2b=5`

`7b-35-2b=5`

`5b=5+35`

`5b=40`

`b=8`

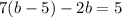
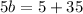
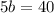
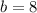
Putting b=8 in (i), we get

`a=8-5`

`a=3`

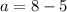
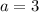
Therefore, the required number is 38.