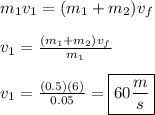Hello!
We can begin by using the Work-Energy theorem. The initial energy is the kinetic energy of the combined mass of the bullet and suspended object, while the final energy is the GPE of the combined objects.
In equations:
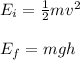
m = combined mass of the bullet and suspended object (0.5 kg)
v = velocity of block system after struck (? m/s)
g = acceleration due to gravity (10 m/s²)
h = final height of combined objects (1.8 m)
Set the two equal (Conservation of Energy) and solve for velocity.
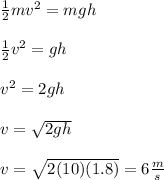
Now, we can use the conservation of linear momentum to solve.
Recall that:

For an inelastic collision (objects stick together):

Let m1 represent the bullet and m2 represent the suspended object.
Initially, the suspended object has no velocity, so v2 = 0. Therefore: