Question

Monique’s son just turned 2 years old and is 34 inches tall. Monique heard that the average boy will grow approximately 2 5/8 inches per year until the ago of 15.

Part A: Write an equation that represents how old Monique’s son will be when he is 50 inches tall. (let X represent the amount of year since age 2)


Part B: How old will Monique’s son be when he is 50 inches tall?

Answer 1

a) The equation that represents how old Monique's son will be when he is 50 inches tall is
`a = 2 + (8)/(21)\cdot (h-34)`.

b) Monique's son will be 8 years old when he is 50 inches tall.

Explanation:

a) From statement we see that Monique's son grows at a constant rate and observes the following linear function:

`h (t) = \dot h \cdot t + h_(o)` (Eq. 1)

Where:

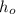`h_(o)` - Initial height of Monique's son, measured in inches.

`\dot h` - Growth rate, measured in inches per year.

`t` - Time, measured in years.

The growth rate of the average boy is:

`\dot h = 2\,(5)/(8)\,(in)/(yr)`

`\dot h = \left((16)/(8)+(5)/(8) \right)\,(in)/(yr)`

`\dot h = (21)/(8) \,(in)/(yr)`

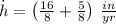
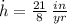
If we know that
`\dot h = (21)/(8) \,(in)/(yr)`,
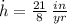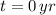`t = 0\,yr` and
`h(t) = 34\,in`, then the initial height of Monique's son is:

`34\,in = \left((21)/(8)\,(in)/(yr) \right)\cdot (0\,yr)+h_(o)`

`h_(o) = 34\,in`

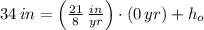
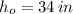
Then, the height of Monique's son as a function of age is represented by:

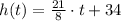`h(t) = (21)/(8)\cdot t +34` (Eq. 2)

The age of Monique's son (
`a`), expressed in years, is represented by the following formula:

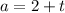`a = 2+t` (Eq. 3)

Now we clear time within (Eq. 2):

`h-34 = (21)/(8)\cdot t`

`t = (8)/(21)\cdot (h-34)`

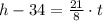
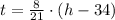
Therefore, the age of Monique's son is modelled after this:

`a = 2 + (8)/(21)\cdot (h-34)` (Eq. 4)

b) If we know that
`h = 50\,in`, then the age of Monique's son will be:

`a = 2 + (8)/(21)\cdot (50-34)`

`a = 8.095\,years.`

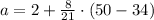
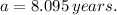
Monique's son will be 8 years old when he is 50 inches tall.