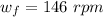Question

A 2.66 kg, 22.25 cm diameter turntable rotates at 238 rpm on frictionless bearings. Two 420 g blocks fall from above, hit the turntable simultaneously at opposite ends of a diagonal, and stick. What is the turntable's angular velocity, in rpm, just after this event

Answer 1

The value is
`w_f = 146 \ rpm`

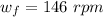
Step-by-step explanation:

From the question we are told that

The mass is
`m = 2.66 \ kg`

The diameter is
`d = 22.25 \ cm = 0.2225 \ m`

The angular speed is
`w_i = 238 \ rpm`

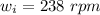
The mass of each of the blocks is
`m_b = 420 \ g = 0.420 \ kg`

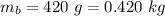
Generally the radius of the turntable is mathematically represented as

`r = (d)/(2)`

=>
`r = (0.2225)/(2)`

=>
`r = 0.11125`

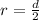
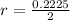
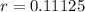
The moment of inertia of the turntable before the blocks fell is mathematically represented as

`I_(i) = (1)/(2) * m * r^2`

=>
`I_(i) = (1)/(2) * 2.66 * (0.11125)^2`

=>
`I_(i) = 0.01646 \ kg\cdot m^2`

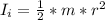
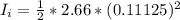
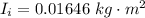
The moment of inertia of the turntable after the blocks fell is mathematically represented as

`I_(f) = (1)/(2) * m * r^2 + 2 m_b * r^2`

=>
`I_(f) = (1)/(2) * 2.66 * (0.11125)^2 + 2 * 0.420 * 0.11125^2`

=>
`I_(f) = 0.02686 \ kg\cdot m^2`

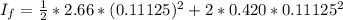
Generally from the law of angular momentum conservation

`L_i = L_f`

Here
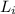`L_i` is the initial angular momentum of the turntable before the blocks fell which is mathematically represented as

`L_i = I_i * w_i`

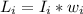
and
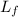`L_f` is the initial angular momentum of the turntable after the blocks fell which is mathematically represented as

`L_i = I_f * w_f`

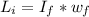
So

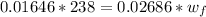
`0.01646* 238 = 0.02686 * w_f`

=>
`w_f = 146 \ rpm`