Answer:
To solve this question I had to search in google the spring constant = 375 N/m!
The velocity of the mass is 1.22 m/s.
Step-by-step explanation:
To solve this question I had to search in google the spring constant = 375 N/m!
We can find the velocity of the mass by energy conservation:
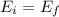
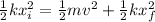
Where:
m: is the mass = 0.500 kg
v: is the velocity of the mass=?
k: is the spring constant = 375 N/m (found in google)
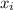 and
and
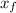 : are the initial and final position of the spring respectively
: are the initial and final position of the spring respectively
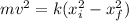
![v = \sqrt{(k(x_(i)^(2) - x_(f)^(2)))/(m)} = \sqrt{(375 N/m[(0.060m)^(2) - (-0.04 m)^(2)])/(0.500 kg)} = 1.22 m/s](https://img.qammunity.org/2021/formulas/physics/college/g6a5c2i1ejcnh3du3tv1ub03oeqd58l5o8.png)
Therefore, the velocity of the mass is 1.22 m/s.
I hope it helps you!