Question

3. Consider an advanced statistics class which consists of 20 Statistics majors, 15 Mathematics majors, 10 Computer Science majors, and 5 Electric Engineering majors. Suppose a random sample of size 10 is drawn from this course without replacement. What is the probability that the sample contains 5 Statistics majors, 3 Mathematics majors, 2 Computer Science majors, and 0 Electric Engineering majors?

Answer 1

Answer: 0.0309

Explanation:

Given: In advanced statistics class, there are 20 Statistics majors, 15 Mathematics majors, 10 Computer Science majors, and 5 Electric Engineering majors.

Total = 20+15+10+5 =50

Number of combinations of selecting r things out of n =
`^nC_r=(n!)/(r!(n-r)!)`

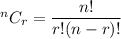
The number of ways to choose a sample of 10 put of 50=
`^(50)C_(10)=(50!)/(10!40!)`

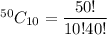
Number of ways to choose 5 Statistics majors, 3 Mathematics majors, 2 Computer Science majors, and 0 Electric Engineering majors =
`^(20)C_5* ^(15)C_3* ^(10)C_2* ^5C_0\\\\=(20!)/(5!15!)*(15!)/(3!12!)*(10!)/(2!8!)*(5!)/(5!0!)`

Required probability =
`((20!)/(5!15!)*(15!)/(3!12!)*(10!)/(2!8!)*(5!)/(5!0!))/((50!)/(10!40!))= 0.0309`

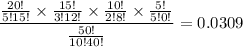
Hence, the required probability = 0.0309