Question

A horizontal 803-N merry-go-round is a solid disk of radius 1.41 m and is started from rest by a constant horizontal force of 49.7 N applied tangentially to the edge of the disk. Find the kinetic energy of the disk after 2.90 s.

Answer 1

The kinetic energy of the disk is 254.4 J.

Step-by-step explanation:

The kinetic energy of the disk is given by:

`K = (1)/(2)I \omega^(2)`

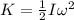
The moment of inertia of the solid disk is:

`I = (1)/(2)mr^(2)`

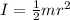
The mass is:

`m = (P)/(g)`

`I = (Pr^(2))/(2g) = (803 N*(1.41 m)^(2))/(2*9.81 m/s^(2)) = 81.4 kgm^(2)`

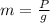
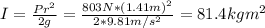
Now, we need to find the angular acceleration as follows:

`\tau = I \alpha`

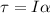
Also, the torque is related to the tangential force:

`\tau = F* r`

`F* r = I \alpha`

`\alpha = (F * r)/(I) = (49.7 N*1.41 m)/(81.4 kg*m^(2)) = 0.86 rad/s^(2)`

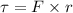
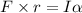
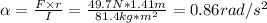
Now, we can find the angular speed:

`\omega_(f) = \omega_(i) + \alpha t`

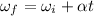
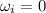`\omega_(i) = 0` since it is started from rest

`\omega_(f) = 0.86 rad\s^(2)*2.90 s = 2.50 rad/s`

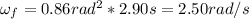
Finally, the kinetic energy of the disk is:

`K = (1)/(2)I \omega^(2) = (1)/(2)81.4 kgm^(2)*(2.50 rad/s)^(2) = 254.4 J`

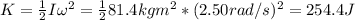
Therefore, the kinetic energy of the disk is 254.4 J.

I hope it helps you!