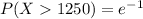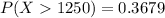Answer:
a)
Mean
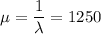
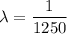
b)
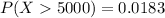
c)
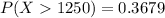
Explanation:
From the given information:
a.)
Mean
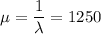
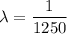
Let consider X to be a random variable that follows an exponential distribution; then:
P(X) = 1 -
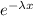 since
since
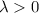
b.)
The required probability that a random chosen customer would spend more than $5,000 can be computed as:
![P(X > 5000) = 1 - \bigg [ 1 - e ^{- (5000)/(1250)} \bigg]](https://img.qammunity.org/2021/formulas/mathematics/college/358ufmjvz1rugkxxptdhy986hdobek219o.png)

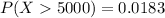
c.)
![P(X > 1250) = 1 - \bigg [ 1 - e ^{- (1250)/(1250)} \bigg]](https://img.qammunity.org/2021/formulas/mathematics/college/j0rt29pct31jigqwo98qth8ekkdwkowjvs.png)