Answer:
The probability that waiting time until the next claim will exceed 4 more days i.e. P(X>6/X>2) = 0.3679
Explanation:
From the given information:
Let consider X to be a random variable that follows an exponential distribution fo the waiting time.
Then;
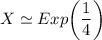 since the mean is distributed between 1 - 4 days
since the mean is distributed between 1 - 4 days
Thus:
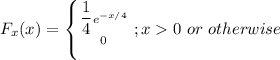
The objective is to determine:
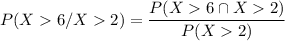
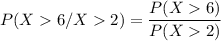
Recall that:
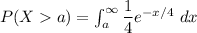
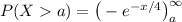
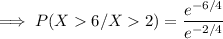
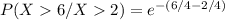
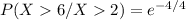
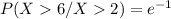
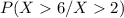 = 0.3678794412
= 0.3678794412
To four decimal places; we have:
The probability that waiting time until the next claim will exceed 4 more days i.e. P(X>6/X>2) = 0.3679