Question

[4F-13] Suppose that waiting time until the next claim is exponentially distributed with mean of 4 days. For last 2 days, there have been no claims. Calculate the probability that waiting time until the next claim will exceed 4 more days (6 days in total). (Round to 4 decimals)

Answer 1

The probability that waiting time until the next claim will exceed 4 more days i.e. P(X>6/X>2) = 0.3679

Explanation:

From the given information:

Let consider X to be a random variable that follows an exponential distribution fo the waiting time.

Then;
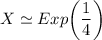`X \simeq Exp \bigg ((1)/(4) \bigg )` since the mean is distributed between 1 - 4 days

Thus:

`F_x(x) = \left \{ {{(1)/(4)e^(-x/4) \atop {0}} \right ; x > 0 \ or \ otherwise`

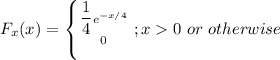
The objective is to determine:

`P(X > 6/ X > 2) = (P(X >6 \cap X >2))/(P(X > 2))`

`P(X > 6/ X > 2) = (P(X >6))/(P(X > 2))`

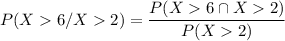
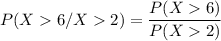
Recall that:

`P(X>a)=\int ^(\infty)_(a)(1)/(4)e^(-x/4) \ dx`

`P(X>a)= \big ( -e ^(-x/4) \big ) ^(\infty)_(a)`

`\implies P(X>6/X>2) = (e^(-6/4))/(e^(-2/4))`

`P(X>6/X>2) = {e^(-(6/4 - 2/4))}`

`P(X>6/X>2) = {e^(-4/4)`

`P(X>6/X>2) = {e^(-1)`

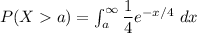
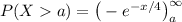
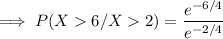
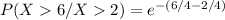
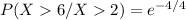
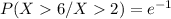
`P(X>6/X>2)` = 0.3678794412

To four decimal places; we have:

The probability that waiting time until the next claim will exceed 4 more days i.e. P(X>6/X>2) = 0.3679