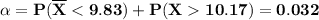The missing values in the question are shown in bold forms below.
A manufacturer is interested in the output voltage of a power supply used in a PC. Output voltage is assumed to be normally distributed, with standard deviation of 0.25 V, and the manufacturer wished to test
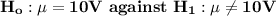 , using n = 10 units. Statistical Tables and Charts
, using n = 10 units. Statistical Tables and Charts
(a) The critical region is
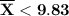 or
or
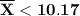 . Find the value of
. Find the value of
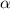
Answer:
∝ = 0.032 (to 3 decimal place)
Explanation:
From the given information:
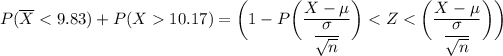

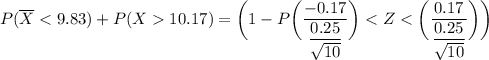
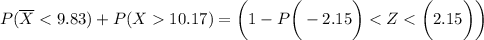
From the z - tables;