Answer:
The percentage of vehicles passing through this construction zone that are exceeding the posted speed limit is 89.44%.
Explanation:
The complete question is:
A construction zone on a highway has a posted speed limit of 40 miles per hour. The speeds of vehicles passing through this construction zone are normally distributed with a mean of 45 miles per hour and a standard deviation of 4 miles per hour. Find the percentage of vehicles passing through this construction zone that are exceeding the posted speed limit. Round your answer to two decimal places.
Solution:
Let X represent the speed of the vehicles passing through the construction zone.
It is provided that X follows a Normal distribution with parameters μ = 45 and σ = 4.
Compute the probability that a randomly selected vehicle exceeds the posted speed limit as follows:

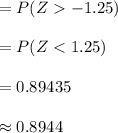
The percentage is, 0.8944 × 100 = 89.44%
Thus, the percentage of vehicles passing through this construction zone that are exceeding the posted speed limit is 89.44%.