Answer:

Step-by-step explanation:
Considering an object that moving about in a circular path, the equation for such centripetal force can be computed as:
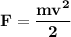
The model for the person can be seen in the diagram attached below.
So, along the horizontal axis, the net force that is exerted on the person is:
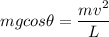
Dividing both sides by "m"; we have :
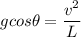
Making "v" the subject of the formula: we have:
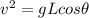

So, when
 = 0; the velocity is maximum
= 0; the velocity is maximum
∴

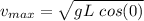
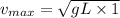

Hence; the maximum walking speed for the person is
