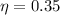Complete Question
A real (non-Carnot) heat engine, operating between heat reservoirs at temperatures of 650 K and 270 K and performs 4.3 kJ of net work and rejects 8.00 kJ of heat in a single cycle. The thermal efficiency of this heat engine is closest to A) 0.35 B) 0.31. C) 0.28. D) 0.38. E) 0.42.
Answer:
The correct option is A
Step-by-step explanation:
From the question we are told that
The first operating temperature is
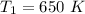
The second operating temperature is

The net workdone is
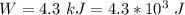 ( output of the engine )
( output of the engine )
The amount of heat energy rejected is
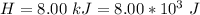
Generally a heat engine convert heat from a high temperature to mechanical energy and then reject the remaining heat so the absorbed by the engine is
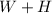
Generally the thermal efficiency is mathematically represented as
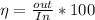
Here out is the output of the engine
and in is the input of the engine
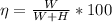
=>
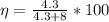
=>