Question

Question 1

Review

Jaden is comparing two cones. The radius of the base of cone A is twice as large as the radius of the base of cone B. The

height of cone B is twice the height of cone A. The volume of cone A is

Answer 1

The volume of cone A is twice the volume of cone B.

Explanation:

The formula that is used to find the volume of a cone is given by :

`V=(1)/(3)\pi r^2 h`

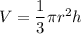
Where

r is radius of cone and h is height

ATQ,

The radius of the base of cone A is twice as large as the radius of the base of cone B. The height of cone B is twice the height of cone A.

`r_A=2r_B\ \text{and}\ h_B=2h_A`

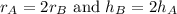
or

`(r_A)/(r_B)={2}\ \text{and}\ (h_A)/(h_B)=(1)/(2)`

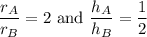
Taking ratios of their volume,

`(V_A)/(V_B)=(1/3\pi r_A^2h_A)/(1/3\pi r_B^2h_B)\\\\(V_A)/(V_B)=((r_A)/(r_B))^2* (h_A)/(h_B)`

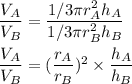
So,

`(V_A)/(V_B)=((r_A)/(r_B))^2* (h_A)/(h_B)\\\\(V_A)/(V_B)=(2)^2* (1)/(2)\\\\(V_A)/(V_B)=2\\\\V_A=2V_B`

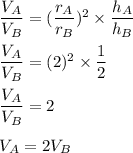
The volume of cone A is twice the volume of cone B.