Answer:
The value is

Step-by-step explanation:
From the question we are told that
The diameter of the ring is
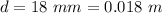
The length of the solenoid is

The diameter of the solenoid is

The number of turns is N = 1500
The change in current in the solenoid is
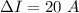
The time taken is
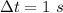
Generally the radius of the ring is
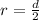
=>
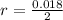
=>
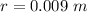
Generally the area of the ring is mathematically represented as
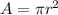
=>
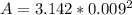
=>
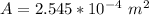
Generally the induced emf is mathematically represented as
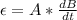
Here

Here
 is the permeability of free space with value
is the permeability of free space with value
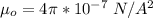
So
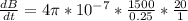
=>
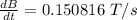
So
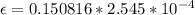
=>
