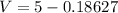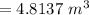Question

Plateau Creek carries 5.0 m^3 /s of water with a selenium (Se) concentration of 0.0015 mg/L. A farmer withdraws water at a certain flowrate (m3 /s) from the creek for irrigation. After using the water, half of the water withdrawn returns to the creek and contains 1.00 mg/L of Se. Fish in the creek are sensitive to Se levels over 0.04 mg/L.

Required:

How much water (m3 /s) can the farmer withdraw from the stream to maintain Se at 0.04 mg/L after the contaminated water is returned to the creek?

Answer 1

The correct answer is "4.8137 m³". The further explanation is given below.

Step-by-step explanation:

Firstly we have to calculate the concentration of Se:

`C = 0.0015 \ mg/L* (1g)/(1000 mg)* (1 \ mol)/(79 \ g)`

`=1.9* 10^(-8) \ mol/L`

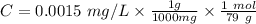
Concentration the fish can take:

`=0.04 \ mg/L* (1 \ g)/(1000mg)* (1 \ mol)/(79 \ g)`

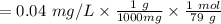
According to the general dilution principle will be:

⇒
`M_1V_1 = M_2V_2`

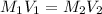
The volume that can take the farmer will be:

`V_2 = 1.9* 10^(-8) M* (5* 10^3 \ L)/(5.1* 10-7 M)`

`=186.27 \ L`

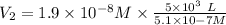
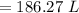
On converting this into m³, we get

=
`0.18627 \ m^3`

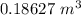
Finally the volume the farmer can remove would be:

`V = 5-0.18627`

`= 4.8137 \ m^3`