Question

An artificial satellite circling the Earth completes each orbit in 130 minutes. (a) Find the altitude of the satellite. Your response differs from the correct answer by more than 10%. Double check your calculations. m (b) What is the value of g at the location of this satellite

Answer 1

a) The altitude of the satellite is approximately 2129 kilometers.

b) The gravitational acceleration at the location of the satellite is 5.517 meters per square second.

Step-by-step explanation:

a) At first we assume that Earth is a sphere with a uniform distributed mass and the satellite rotates on a circular orbit at constant speed. From Newton's Law of Gravitation and definition of uniform circular motion, we get the following identity:

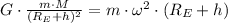`G\cdot (m\cdot M)/((R_(E)+h)^(2)) = m\cdot \omega^(2)\cdot (R_(E)+h)` (Eq. 1)

Where:

`G` - Gravitational constant, measured in newton-square meters per square kilograms.

`m` - Mass of the satellite, measured in kilograms.

`M` - Mass of the Earth, measured in kilograms.

`\omega` - Angular speed of the satellite, measured in radians per second.

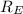`R_(E)` - Radius of the Earth, measured in meters.

`h` - Height of the satellite above surface, measured in meters.

Then, we simplify the formula and clear the height above the surface:

`G\cdot M = \omega^(2)\cdot (R_(E)+h)^(3)`

`(R_(E)+h)^(3) =(G\cdot M)/(\omega^(2))`

`R_(E)+h = \sqrt[3]{(G\cdot M)/(\omega^(2)) }`

`h = \sqrt[3]{(G\cdot M)/(\omega^(2)) }-R_(E)`

From Rotation physics, we know that angular speed is equal to:

`\omega = (2\pi)/(T)` (Eq. 2)

And (Eq. 1) is now expanded:

`h = \sqrt[3]{(G\cdot M\cdot T^(2))/(4\pi^(2)) }-R_(E)` (Eq. 3)

If we know that
`G = 6.674* 10^(-11)\,(N\cdot m^(2))/(kg^(2))`,
`M = 5.972* 10^(24)\,kg`,
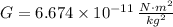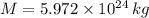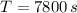`T = 7800\,s` and
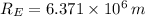`R_(E) = 6.371* 10^(6)\,m`, then the altitude of the satellite is:

`h = \sqrt[3]{(\left(6.674* 10^(-11)\,(N\cdot m^(2))/(kg^(2)) \right)\cdot (5.972* 10^(24)\,kg)\cdot (7800\,s)^(2))/(4\pi^(2)) }-6.371* 10^(6)\,m`

`h\approx 2.129* 10^(6)\,m`

`h \approx 2.129* 10^(3)\,km`

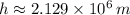
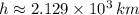
The altitude of the satellite is approximately 2129 kilometers.

b) The value for the gravitational acceleration of the satellite (
`g`), measured in meters per square second, is derived from the Newton's Law of Gravitation, that is:

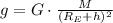`g = G\cdot (M)/((R_(E)+h)^(2))` (Eq. 4)

If we know that
`G = 6.674* 10^(-11)\,(N\cdot m^(2))/(kg^(2))`,
`M = 5.972* 10^(24)\,kg`,
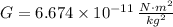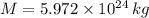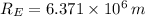`R_(E) = 6.371* 10^(6)\,m` and
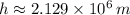`h\approx 2.129* 10^(6)\,m`, then the value of the gravitational acceleration at the location of the satellite is:

`g = (\left(6.674* 10^(-11)\,(N\cdot m^(2))/(kg^(2)) \right)\cdot (5.972* 10^(24)\,kg))/((6.371* 10^(6)\,m+2.129* 10^(6)\,m)^(2))`

`g = 5.517\,(m)/(s^(2))`

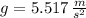
The gravitational acceleration at the location of the satellite is 5.517 meters per square second.