Answer:
(a)
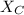 = 139.8 Ω
= 139.8 Ω
(b)
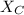 = 245 Ω
= 245 Ω
(c)
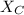 = -24113.8 Ω
= -24113.8 Ω
Step-by-step explanation:
Given that: R = 245 Ω,
 = 385 Ω.
= 385 Ω.
But,
cos(ϕ) =
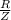
Where Z is the impedance in the circuit.
(a) when cos(ϕ) = 0.707,
0.707 =
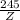
⇒ Z =
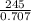
= 346.5346
The impedance of the circuit, Z, is 346.6 Ω.
But,
Z =
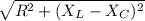
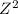 =
=
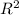 +
+
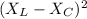
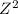 -
-
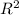 =
=
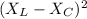
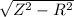 =
=
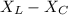
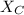 =
=
 -
-
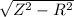
= 385 -
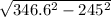
= 385 - 245.2
= 139.8
Therefore,
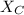 is 139.8 Ω.
is 139.8 Ω.
(b) When cos(ϕ) = 1.00, then;
cos(ϕ) =
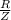
1.00 =
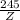
Z = 245 Ω
The impedance of the circuit is 245 Ω.
So that;
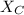 =
=
 -
-
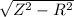
= 245 - 0
= 245 Ω
The capacitive reactance is 245 Ω. In this circuit, resonance occurs since
 =
=
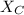 .
.
(c) When cos(ϕ) = 1.00 x
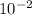 ,
,
cos(ϕ) =
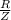
1.00 x
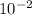 =
=
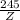
Z = 24500 Ω
So that:
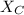 =
=
 -
-
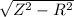
= 385 -
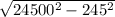
= 385 - 24498.8
= -24113.8 Ω
The capacitive reactance is -24113.8 Ω. This implies that the voltage lags behind the current.