Answer:
(a) The Japanese Company will be preferred due to less charges.
(b) The Italian Company will be preferred due to less charges.
(c) The Italian Company will be preferred due to less charges.
(d) The Japanese Company will be preferred due to less charges.
Explanation:
The complete question is:
Two different suppliers are competing to supply a particular part for a new Boeing airliner. The Japanese supplier charges J(n) dollars for n parts whereas the Italian supplier charges I(n) dollars for n parts.
(a) Which supplier should be used to supply a large number of parts if
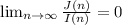
(b) Which supplier should be used to supply a large number of parts if
 ∞
∞
(c) Which supplier should be used to supply a large number of parts if
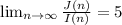
(d) Which supplier should be used to supply a large number of parts if

ANSWERS:
(a)
Applying the given limits will result in:
J(∞)/I(∞) = 0
So either, I(∞) must be ∞ or J(∞) must be zero in order to give a result of zero.
Hence, the Japanese Company will be preferred due to less charges.
(b)
Applying the given limits will result in:
J(∞)/I(∞) = ∞
So either, J(∞) must be ∞ or I(∞) must be zero in order to give a result of infinity.
Hence, the Italian Company will be preferred due to less charges.
(c)
Applying the given limits will result in:
J(∞)/I(∞) = 5
J(∞) = 5*I(∞)
So the charges of Japanese Company are 5 times the charges of Italian Company,
Hence, the Italian Company will be preferred due to less charges.
(d)
Applying the given limits will result in:
J(∞)/I(∞) = 0.2
J(∞) = I(∞)/5
I(∞) = 5*J(∞)
So the charges of Italian Company are 5 times the charges of Japanese Company,
Hence, the Japanese Company will be preferred due to less charges.