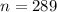Complete Question
Executives of a supermarket chain are interested in the amount of time that customers spend in the stores during shopping trips. The executives hire a statistical consultant and ask her to determine the mean shopping time,u , of customers at the supermarkets. The consultant will collect a random sample of shopping times at the supermarkets and use the mean of these shopping times to estimate .u. Assuming that the standard deviation of the population of shopping times at the supermarkets is 26 minutes, what is the minimum sample size she must collect in order for her to be 95% confident that her estimate is within 3 minutes of
 ? Carry your intermediate computations to at least three decimal places. Write your answer as a whole number (and make sure that it is the minimum whole number that satisfies the requirements).
? Carry your intermediate computations to at least three decimal places. Write your answer as a whole number (and make sure that it is the minimum whole number that satisfies the requirements).
Answer:
The sample size is
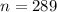
Explanation:
From the question we are told that
The standard deviation is
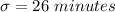
The margin of error is
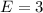
From the question we are told the confidence level is 95% , hence the level of significance is
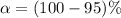
=>

Generally from the normal distribution table the critical value of
 is
is
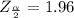
Generally the sample size is mathematically represented as
![n = [\frac{Z_{(\alpha )/(2) } * \sigma }{E} ] ^2](https://img.qammunity.org/2021/formulas/mathematics/college/j63im5d7bkeqfrgf56wd02g4fvud45p15n.png)
=>
![n = [( 1.96 * 26 )/(3) ] ^2](https://img.qammunity.org/2021/formulas/mathematics/college/llerjd84bepvj5mj8u4h0p3hbxy3mz45xg.png)
=>