Question

Problem 10-9 A sample of 40 observations is taken from a population of unknown mean wherein the standard deviation is assumed to be 5 grams. The computed value of the sample mean is 38.0 grams. Construct confidence intervals for each of the following levels of confidence: (a) 90% Confidence Interval

Answer 1

Answer: (36.7, 39.3)

Explanation:

Confidence interval for population mean:

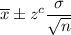`\overline{x}\pm z^c(\sigma)/(√(n))` , where n= sample size,
`\overline{x}`= sample mean,
`\sigma` = population standard deviation,
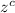`z^c` = critical z value.

Given: n= 40 ,
`\sigma=5\ g,\ \ \ \overline{x} = 38.0\ g`

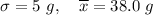
Critical z-value for 90% confidence = 1.645

Then, required confidence interval:

`38.0\pm(1.645)(5)/(√(40))\\\\= 38.0\pm (1.645)(0.79057)\\\\\approx38.0\pm1.30\\\\= (38-1.30,\ 38+1.30)=(36.7,\ 39.3)`

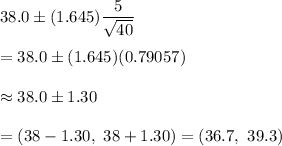
Hence, a 90% Confidence Interval = (36.7, 39.3)