Answer: The running time should at least 119.32 seconds to be in the top 5% of runners.
Explanation:
Let X= random variable that represents the running time of men between 18 and 30 years of age.
As per given, X is normally distrusted with mean
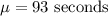 and standard deviation
and standard deviation
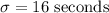 .
.
To find: x in top 5% i.e. we need to find x such that P(X<x)=95% or 0.95.
i.e.
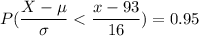
![P(Z<(x-93)/(16))=0.95\ \ \ \ \ [Z=(X-\mu)/(\sigma)]](https://img.qammunity.org/2021/formulas/mathematics/college/s98gqk5ibc3uak6ffeg404icw9xz538bm4.png)
Since, z-value for 0.95 p-value ( one-tailed) =1.645
So,
Hence, the running time should at least 119.32 seconds to be in the top 5% of runners.