Answer:
The translation rule is described by
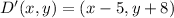 .
.
Explanation:
According to Linear Algebra, a translation consists in sum a given vector (original point in this case) with another vector (translation vector). We can define translation as follows:
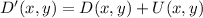 (Eq. 1)
(Eq. 1)
Where:
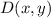 - Original vector with respect to origin, dimensionless.
- Original vector with respect to origin, dimensionless.
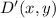 - Translated vector with respect to origin, dimensionless.
- Translated vector with respect to origin, dimensionless.
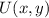 - Translation vector with respect to original vector, dimensionless.
- Translation vector with respect to original vector, dimensionless.
From (Eq. 1) we get that translation vector is:
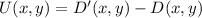
If we know that
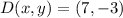 and
and
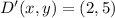 , then the translation vector is:
, then the translation vector is:
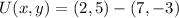
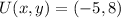
And we find the translation rule by assuming that
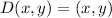 and
and
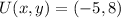 in (Eq. 1):
in (Eq. 1):
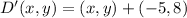
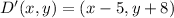
The translation rule is described by
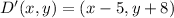 .
.