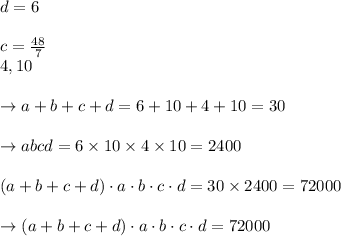Answer:
The answer is "72000".
Explanation:
Given:
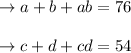
A & b are interchangeable here now and must both be equal.
b is unusual, so ab is strange if an is strange
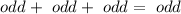 Whereas 76 are also
Whereas 76 are also
Even if an is odd, ab is even
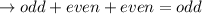
So a & b must be uniform
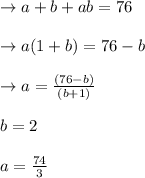 not possible
not possible
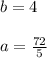 not possible
not possible


The same must be valid and interchangeable as above
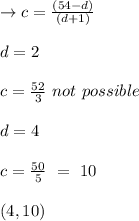 solution
solution