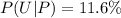Question

Suppose a drug test is 93% sensitive and 87% specific. That is, the test will produce 93% true positive results for drug users and 87% true negative results for non-drug users. Suppose that 1.8% of people are users of the drug. If a randomly selected individual tests positive, what is the probability he or she is a user

Answer 1

The probability is
`P(U | P ) = 11.6 \%`

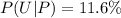
Explanation:

Generally a true positive means that the person tested is a drug user and he/she test positive to the test

while true negative mean that the person tested is not a drug user and he/she test negative to the test

From the question we are told that

The probability that a person test positive to the drug test given that the person is a drug user is

`P(P | U ) = 0.93`

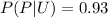
Here P => event that a person test positive to the drug test

U => event that the person is a drug user

The probability that a person test negative to the drug test given that the person is not a drug user is

`P(N | S ) = 0.87`

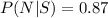
Here N => event that a person test negative to the drug test

S => event that the person is not a drug user

The probability that a person is a drug user is

`P(U) = 0.018`

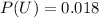
Generally the probability that a person test positive to the test given that the person is a non- user is

`P(P | S ) = 1 - 0.87`

=>
`P(P | S ) = 0.13`

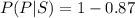
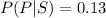
Generally the probability that a person is a non user of drug is

`P(S) = 1 - 0.018`

=>
`P(S) = 0.982`

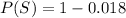
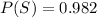
Generally the probability that a person test positive to the drug test is mathematically evaluated as

`P(P) = P(P | U) * P(U ) + P(P | S ) * P(S)`

=>
`P(P) = 0.93 * 0.018 + 0.13 * 0.982`

=>
`P(P) = 0.1444`

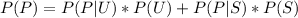
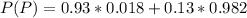
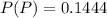
Generally the probability a person is a user given that he or she tested positive is mathematically represented as

`P(U | P ) = (P(P |U ) * P(U))/(P(P))`

=>
`P(U | P ) = (0.93 * 0.018 )/(0.1444)`

=>
`P(U | P ) = 0.116`

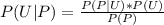
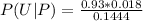
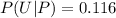
Converting to percentage

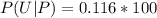
`P(U | P ) = 0.116 * 100`

=>
`P(U | P ) = 11.6 \%`