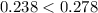Complete Question
The 2003 Statistical Abstract of the United States reported the percentage of people 18 years of age and older who smoke. Suppose that a study designed to collect new data on smokers and non smokers uses a preliminary estimate of the proportion who smoke of 0.30.
a. How large a sample should be taken to estimate the proportion of smokers in the population with a margin of error of 0.02? use 95% confidence.
b. Assume that the study uses your sample size recommendation in part (a) and finds 520 smokers. What is the point estimate of the proportion of smokers in the population?
c. What is the 95% confidence interval for the proportion of smokers in the population?
Answer:
a

b
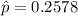
c
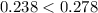
Explanation:
Considering question a
From the question we are told that
The margin of error is

The preliminary estimate of the proportion who smoke is
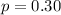
From the question we are told the confidence level is 95% , hence the level of significance is
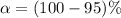
=>

Generally from the normal distribution table the critical value of
 is
is
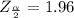
Generally the sample size is mathematically represented as
![n = [ \frac{Z_{(\alpha )/(2) } }{E} ] ^2 * p(1 - p )](https://img.qammunity.org/2021/formulas/mathematics/college/s4ryx6fm4t21hbh3x8f0aet4tnv5fd65fs.png)
=>
![n = [ (1.96 )/(0.02) ] ^2 * 0.30(1 - 0.30 )](https://img.qammunity.org/2021/formulas/mathematics/college/bos3hk1bthqu8h1hcot7v4cov0nsd5af94.png)
=>

Considering question b
From the question we are told that
The number of smokers is k = 520
Generally the point estimate of the proportion of smokers in the population is mathematically represented as
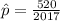
=>
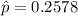
Considering question c
Generally 95% confidence interval is mathematically represented as
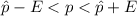
=>

=>