Answer: (8.64, 12.7)
Explanation:
When population standard deviation is unknown then, confidence interval for population mean is given by :-
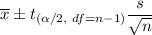
, where n= sample size , s= sample standard deviation,
 = sample mean,
= sample mean,
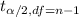 = two tailed t value for confidence level of 1-
= two tailed t value for confidence level of 1-
 and degree of freedom = 1-n.
and degree of freedom = 1-n.
Given: n= 10 , s= 2.27 kg ,
 kg
kg
df = 10-1=9
For 98% confidence, significance level =
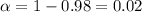
T-critical value:
![t_((0.02/2,9))=t_(0.01,9)=2.8214\ \ \ [\text{By student's t-distribution table}]](https://img.qammunity.org/2021/formulas/mathematics/college/5gt8um6ae08wfzek29p2fg8h767p4nhbjs.png)
Now, 98% confidence interval for the true mean weight of Trek mountain bikes will be :

Hence, a 98% confidence interval for the true mean weight of Trek mountain bikes= (8.64, 12.7)