Question

The popular sport of mounting biking involves riding bikes off-road, often over very rough terrain. Trek is a leading manufacturer of mountain bikes, specially designed for durability and performance. A random sample of 10 Trek mountain bikes was obtained and each was carefully weighed. The resulting data yielded a sample mean of 10.67 kg and a sample standard deviation of 2.27 kg. Assume the underlying distribution of weights is normal. Find a 98% confidence interval for the true mean weight of Trek mountain bikes. (Round your answers to 2 decimal places.)

Answer 1

Answer: (8.64, 12.7)

Explanation:

When population standard deviation is unknown then, confidence interval for population mean is given by :-

`\overline{x}\pm t_((\alpha/2,\ df=n-1))(s)/(√(n))`

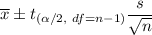
, where n= sample size , s= sample standard deviation,
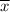`\overline{x}` = sample mean,
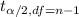`t_(\alpha/2, df=n-1)` = two tailed t value for confidence level of 1-
`\alpha` and degree of freedom = 1-n.

Given: n= 10 , s= 2.27 kg ,
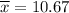`\overline{x}=10.67` kg

df = 10-1=9

For 98% confidence, significance level =
`\alpha=1-0.98=0.02`

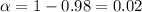
T-critical value:
`t_((0.02/2,9))=t_(0.01,9)=2.8214\ \ \ [\text{By student's t-distribution table}]`

Now, 98% confidence interval for the true mean weight of Trek mountain bikes will be :

`10.67\pm (2.8214)(2.27)/(√(10))\\\\=10.67\pm2.03\\\\ =(10.67-2.03,\ 10.67+2.03)\\\\=(8.64,\ 12.7)`

Hence, a 98% confidence interval for the true mean weight of Trek mountain bikes= (8.64, 12.7)