Question

Suppose a study estimated the population mean for a variable of interest using a ​% confidence interval. If the width of the estimated 99%confidence interval​ (the difference between the upper limit and the lower​ limit) is and the sample size used in estimating the mean is ​, what is the population standard​ deviation? The population standard deviation is nothing.

Answer 1

Complete Question

suppose a study estimated the population mean for a variable of interest using a 99% confidence interval. If the width of the estimated confidence interval( the difference between the upper limit and the lower limit) is 600 and the sample size used in estimating the mean is 1000, what is the population standard deviation?

Answer:

The value is
`\sigma = 3677`

Explanation:

From the question we are told that

The width of the 99% confidence interval is w = 600

The sample size is n = 1000

From the question we are told the confidence level is 99% , hence the level of significance is

`\alpha = (100 - 99) \%`

=>
`\alpha = 0.01`

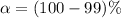
Generally from the normal distribution table the critical value of
`(\alpha )/(2)` is

`Z_{(\alpha )/(2) } =  2.58`

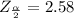
Generally the margin of error is mathematically evaluated as

`E = (w)/(2)`

=>
`E = (600)/(2)`

=>
`E = 300`

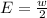
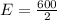
Generally this margin of error can be mathematically represented as

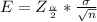
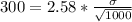
`E = Z_{(\alpha )/(2) } * (\sigma)/(√(n) )`

=>
`300 = 2.58 * (\sigma)/(√(1000) )`

=>
`\sigma = 3677`