Question

Suppose the number of a particular type of bacteria in samples of 1 milliliter (ml) of drinking water tend to be approximately normally distributed, with a mean of 85 and a standard deviation of 9. What is the probability that a given 1-ml will contain more than 100 bacteria

Answer 1

Answer: 0.0475

Explanation:

Let x = random variable that represents the number of a particular type of bacteria in samples of 1 milliliter (ml) of drinking water, such that X is normally distributed.

Given:
`\mu=85,\ \ \sigma=9`

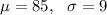
The probability that a given 1-ml will contain more than 100 bacteria will be:

`P(X>100)=P((X-\mu)/(\sigma)>(100-85)/(9))\\\\=P(Z>1.67)\ \ \ \ [Z=(X-\mu)/(\sigma)]\\\\=1-P(Z<1.67)\ \ \ [P(Z>z)=1-P(Z<z)]\\\\=1- 0.9525=0.0475`

∴The probability that a given 1-ml will contain more than 100 bacteria

0.0475.