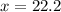Complete Question
The SAT and ACT college entrance exams are taken by thousands of students each year. The mathematics portions of each of these exams produce scores that are approximately normally distributed. In recent years, SAT mathematics exam scores have averaged 480 with standard deviation 100. The average and standard deviation for ACT mathematics scores are 18 and 6, respectively.
a An engineering school sets 550 as the minimum SAT math score for new students. What percentage of students will score below 550 in a typical year
b What would the engineering school set as a comparable standard on the ACT math test?
Answer:
a

b
The minimum for ACT is
Explanation:
From the question we are told that
The mean for SAT is
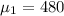
The standard deviation for SAT is
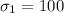
The mean for ACT is
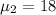
The standard deviation for

Generally the proportion of students will score below 550 in a typical year is mathematically represented as
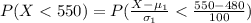
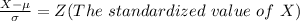
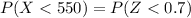
From the z table the area under 0.7 to the left is
=>
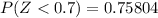
So
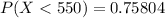
Converting to percentage
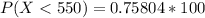

Generally the score which the engineering school would set as a comparable standard on the ACT math test is mathematically evaluated as
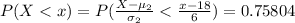
=>
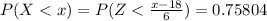
From the normal distribution table the critical value of 0.75804 is
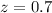
So
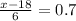
=>