Answer:
Velocity is
 and Acceleration is 8
and Acceleration is 8
Explanation:
Equation of position of the particle
r(t) = (8sint)i + (8cost)j + (8t)k
1) Velocity of the particle is
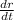
V(t) = dr/dt = (8cost)i + (-8sint)j + 8k
2) Acceleration of the particle will be
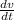
A(t) = dv/dt = (-8sint)i + (-8cost)j + 0k
velocity of the particle at t=
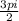
V(
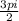 ) = (0)i + (8)j + 8k =
) = (0)i + (8)j + 8k =
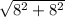 =
=

acceleration at t=
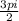
A(
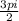 ) = (8)i + (0)j +0k =
) = (8)i + (0)j +0k =
 = 8
= 8