The slope of the line, representing the cost of apples, is
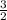 . Further details, such as the y-intercept, are needed to determine the cost for 1 pound.
. Further details, such as the y-intercept, are needed to determine the cost for 1 pound.
To find the slope m of the line passing through the points (0,0) and (2,3), you can use the formula:
![\[ m = \frac{{\text{{change in }} y}}{{\text{{change in }} x}} \]](https://img.qammunity.org/2021/formulas/mathematics/high-school/567zcyds73g8iv4c0h9brhgu3xeaoxymad.png)
Given the points (0,0) and (2,3):
![\[ \text{{change in }} y = 3 - 0 = 3 \]](https://img.qammunity.org/2021/formulas/mathematics/high-school/lq5zt6tgss0unhnmugr6kv58c6qd4t4wbo.png)
![\[ \text{{change in }} x = 2 - 0 = 2 \]](https://img.qammunity.org/2021/formulas/mathematics/high-school/ad0b8m4cjknh6q6h7xpk997cpyx3lt3936.png)
Now substitute these values into the slope formula:
![\[ m = (3)/(2) \]](https://img.qammunity.org/2021/formulas/mathematics/high-school/5axpzy4pvcv8jk9mx8u7zg2um9iejt4anz.png)
So, the slope of the line is
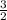 . This represents the rate of change of cost per pound of apples. If you have more information, like the y-intercept, you can use the slope-intercept form y = mx + b to find the cost for 1 pound of apples.
. This represents the rate of change of cost per pound of apples. If you have more information, like the y-intercept, you can use the slope-intercept form y = mx + b to find the cost for 1 pound of apples.