Question

PLEASE HELP W CALC!!

ONLY #14 but you need to look at the the question (not the answer) in 13 to answer 14

14. Write but do not evaluate the integral which can be used to find the volume which results when region R in problem 13 is revolves around the line x=4

Answer 1

`\displaystyle V = \pi \int_0^(1.835)\left[ 4 - y^2\right]^2 - \left[ 4-√(4(y+1))\right]^2\, dy`

Explanation:

We can use the washer method. Because the axis of revolution is vertical, our representative rectangle is horizontal. Recall that:

`\displaystyle V = \pi \int_a^b \left[ R(y)\right] ^2 - \left[r(y)\right]^2 \, dy`

Solve each equation as a function of y:

`\displaystyle \begin{aligned} y & = √(x) \\ \\ x_1 & = y^2\end{aligned}`

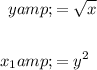
And:

`\displaystyle \begin{aligned} y & = (1)/(4)x^2 - 1 \\ \\ x_2 & = \pm√(4(y+1)) \\ \\ & = √(4(y+1))\end{aligned}`

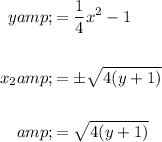
The outer radius R is simply (4 - x₁) and the inner radius r is (4 - x₂). The point of intersection is (3.368, 1,835), so our limits of integration are from y = 0 to y = 1.835.

Therefore, the integral that represents the region being revolved around

x = 4 is:

`\displaystyle V = \pi \int_0^(1.835)\left[ 4 - y^2\right]^2 - \left[ 4-√(4(y+1))\right]^2\, dy`