Answer:
Z-score = 3.73
Yes, the maximum value (21) in this data set is a high outlier.
Explanation:
I'll solve for what you haven't done yet, z-score and whether or not the maximum is an outlier.
Z-score tells us how many standard deviations a value is above or below the mean. The formula for z-score is
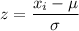 .
.
Substituting
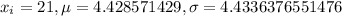 , we get
, we get
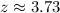 .
.
To determine if a value is an outlier, we use IQR, or Interquartile Range. If a value is lower than
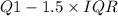 or higher than
or higher than
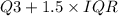 , then we say it is an outlier.
, then we say it is an outlier.
With the value of 21, clearly we are only worried about it being a high outlier. Q1 is the median of the first half of the data and Q3 is the median of the second half. In this case, Q1 is 2 and Q3 is 6.5. IQR is equal to Q3-Q1, or 4.5 in this case.
Therefore, the higher limit for outliers is
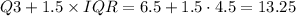 . Any values above 13.25 are considered high outliers. Therefore, the maximum value of 21 is a high outlier.
. Any values above 13.25 are considered high outliers. Therefore, the maximum value of 21 is a high outlier.