Question

If the measure of angle B=35 degrees, a=43, and c=19 then find the measure of angle A

Answer 1

Answer: 123.3364311 degrees approximately

Round that value however your teacher instructs.

==========================================================

Step-by-step explanation:

Use the law of cosines to find side b

`b^2 = a^2 + c^2 - 2*a*c*\cos(B)\\\\b^2 = 43^2 + 19^2 - 2*43*19*\cos(35)\\\\b^2 \approx 871.5055596\\\\b \approx √(871.5055596)\\\\b \approx 29.521273\\\\`

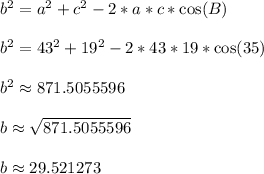
Now use the law of sines to find angle A.

`(\sin(A))/(a) = (\sin(B))/(b)\\\\(\sin(A))/(43) \approx (\sin(35))/(29.521273)\\\\\sin(A)\approx 43*(\sin(35))/(29.521273)\\\\\sin(A) \approx 0.8354581\\\\A \approx \sin^(-1)(0.8354581) \text{ or } A \approx 180-\sin^(-1)(0.8354581)\\\\A \approx 56.6635689^(\circ) \text{ or } A \approx 123.3364311^(\circ)\\\\`

Due to the side angle side (SAS) congruence theorem, we know that only one triangle is possible (notice angle B is between sides 'a' and c). This means only one of those values for angle A is possible.

The question is: Which one?

Well if you were to use the converse of the pythagorean theorem, then you'll find that the triangle is obtuse.

For any obtuse triangle, the longest side is always opposite the obtuse angle (aka the angle over 90 degrees). The side a = 43 is the longest side of this particular triangle.

This means angle A must be obtuse and the only possibility is that angle A = 123.3364311 degrees approximately.