Answer:
b.

General Formulas and Concepts:
Pre-Algebra
Order of Operations: BPEMDAS
- Brackets
- Parenthesis
- Exponents
- Multiplication
- Division
- Addition
- Subtraction
Algebra I
- Functions
- Function Notation
- Exponential Rule [Rewrite]:
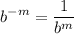
- Exponential Rule [Root Rewrite]:
![\displaystyle \sqrt[n]{x} = x^{(1)/(n)}](https://img.qammunity.org/2021/formulas/mathematics/high-school/ovswe6woyxmv3hfdn80atr35ajxkh4i9t1.png)
Calculus
Derivatives
Derivative Notation
Basic Power Rule:
- f(x) = cxⁿ
- f’(x) = c·nxⁿ⁻¹
Derivative Rule [Chain Rule]:
![\displaystyle (d)/(dx)[f(g(x))] =f'(g(x)) \cdot g'(x)](https://img.qammunity.org/2021/formulas/mathematics/college/ljowxevzhh8dk8mfdheam579ywk5jvteyi.png)
Explanation:
Step 1: Define
Identify
![\displaystyle H(x) = \sqrt[3]{F(x)}](https://img.qammunity.org/2021/formulas/mathematics/college/bs9nmhchyhunsr8yyu4etzrp5q3ma2tpil.png)
Step 2: Differentiate
- Rewrite function [Exponential Rule - Root Rewrite]:
![\displaystyle H(x) = [F(x)]^\bigg{(1)/(3)}](https://img.qammunity.org/2021/formulas/mathematics/college/aw6qwzje4uo176nxzhz3lwxylhmxdsdqlk.png)
- Chain Rule:
![\displaystyle H'(x) = (d)/(dx) \bigg[ [F(x)]^\bigg{(1)/(3)} \bigg] \cdot (d)/(dx)[F(x)]](https://img.qammunity.org/2021/formulas/mathematics/college/pero66h57v8rhfyhfjo4pdarc3fpg0fdk7.png)
- Basic Power Rule:
![\displaystyle H'(x) = (1)/(3)[F(x)]^\bigg{(1)/(3) - 1} \cdot F'(x)](https://img.qammunity.org/2021/formulas/mathematics/college/1ek73szctqyy7apea9vpsu9kgbmx0z32rn.png)
- Simplify:
![\displaystyle H'(x) = (F'(x))/(3)[F(x)]^\bigg{(-2)/(3)}](https://img.qammunity.org/2021/formulas/mathematics/college/g4hse7x0suwwe7rzrvdnlgfo43p5lgwsaj.png)
- Rewrite [Exponential Rule - Rewrite]:
![\displaystyle H'(x) = \frac{F'(x)}{3[F(x)]^\bigg{(2)/(3)}}](https://img.qammunity.org/2021/formulas/mathematics/college/5ib4zs61p0ap9shv3ibmp3coohn9fvce8t.png)
Step 3: Evaluate
- Substitute in x [Derivative]:
![\displaystyle H'(5) = \frac{F'(5)}{3[F(5)]^\bigg{(2)/(3)}}](https://img.qammunity.org/2021/formulas/mathematics/college/5qu1g10c3axv2vlfxv56ae9tsk8qrng8xj.png)
- Substitute in function values:
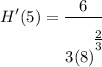
- Exponents:
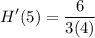
- Multiply:
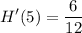
- Simplify:
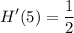
Topic: AP Calculus AB/BC (Calculus I/I + II)
Unit: Derivatives
Book: College Calculus 10e