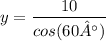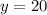Answer:
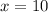
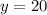
Explanation:
Note:
(sin, cos, tan) Formulas:
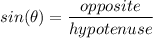
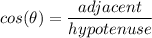
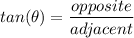
To find the value of

1) Using
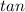 formula
formula
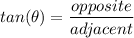
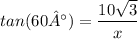
2) Multiply both sides by

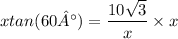
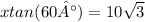
3) Divide both side by
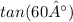
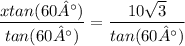
4) Calculate
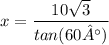
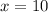
To find the value of
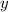
1) Using
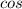 formula
formula
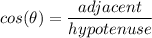
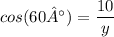
2) Multiply both sides by
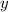
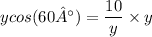
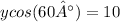
3) Divide both side by
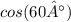
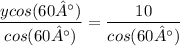
4) Calculate