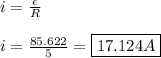Question

A coil with 50 turns of wire is wrapped around a hollow tube with an area of 3.6 m2. Each turn has the same area as the tube. A uniform magnetic field is applied at a right angle to the plane of the coil. If the field increases uniformly from 0.00 T to 0.88 T in 1.85 s, find the magnitude of the induced emf in the coil. If the resistance in the coil is 5.0 Ω, find the magnitude of the induced current in the coil.

Answer 1

Hi there!

Using Faraday's and Lenz's Law:

`\epsilon = -N(d\Phi_B)/(dt)`

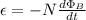
ε = Induced emf (V)

N = number of loops/turns
Φ = Magnetic flux (Wb)

Magnetic flux is given as:

`\Phi_B = \oint B \cdot dA = B\cdot A`
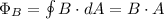
Since the area of the loops remains constant, we can take area out of the time derivative. Thus:

`(d\Phi_B)/(dt) = A * (dB)/(dt) = A * (\Delta B)/(\Delta t)`

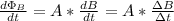
Also, since the magnetic field is applied at a right angle to the plane of the coil, that means that the field is PARALLEL to the area vector of the plane of the coil. (points normal to the surface). This means we can disregard the dot product since cos(180) = 1.

Plug in the given values.

`\epsilon = - 50 * 3.6 * (0.88 - 0)/(1.85) = -85.622 V`

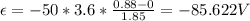
The negative sign simply means that the induced emf is in the opposite direction in order to oppose the increase in magnetic flux, so the magnitude is simply:

`\epsilon = \boxed{85.622 V}`

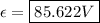
For the current, we can use Ohm's Law:

`i = (\epsilon)/(R)\\\\i = (85.622)/(5) = \boxed{17.124 A}`