Question

An architect wants to draw a rectangle with a diagonal of 20 inches. The length of the rectangle is to be 8 inches more than twice the width. What dimensions should she make the rectangle?

Answer 1

Given:

Diagonal of the rectangle = 20 inches

The length of the rectangle is to be 8 inches more than twice the width.

To find:

The dimensions of the rectangle.

Solution:

Let width of the rectangle be x inches.

Then, length = 2x+8 inches

We know that, diagonal of a rectangle is

`Diagonal=√(length^2+width^2)`

`20=√((2x+8)^2+x^2)`

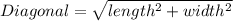
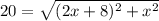
Taking square both sides.

`400=4x^2+32x+64+x^2`

`0=5x^2+32x+64-400`

`0=5x^2+32x-336`

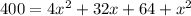
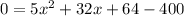
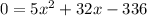
Splitting the middle term, we get

`5x^2+60x-28x-336=0`

`5x(x+12)-28(x+12)=0`

`(x+12)(5x-28)=0`

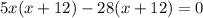
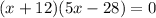
Using zero product property, we get

`x=-12, x=(28)/(5)=5.6`

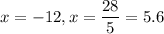
Side length cannot be negative. So, only value of x is
`5.6`.

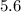Now,

Width = 5.6 inches

Length
`=2(5.6)+8`

`=11.2+8`

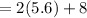
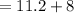
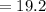`=19.2` inches

Therefore, the length of rectangle is 19.2 inches and width of the rectangle is 5.6 inches.