Given:
Diagonal of the rectangle = 20 inches
The length of the rectangle is to be 8 inches more than twice the width.
To find:
The dimensions of the rectangle.
Solution:
Let width of the rectangle be x inches.
Then, length = 2x+8 inches
We know that, diagonal of a rectangle is
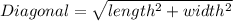
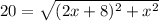
Taking square both sides.
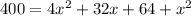
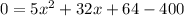
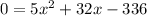
Splitting the middle term, we get
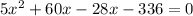
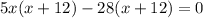
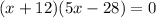
Using zero product property, we get
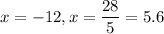
Side length cannot be negative. So, only value of x is
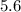 .
.
Now,
Width = 5.6 inches
Length
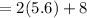
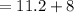
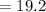 inches
inches
Therefore, the length of rectangle is 19.2 inches and width of the rectangle is 5.6 inches.