Answer:
The last graph is your answer.
Explanation:
The midline of the function should be in between the highest and lowest y value.
Here's the midline should be at y=-1
Let find where our zeroes occur at

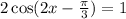

Take the inverse cosine of both sides
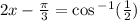
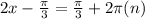
Or
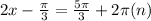
Solve for x. in both scenarios
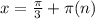
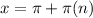
So our zeroes occur at pi/3, and pi, and every pi units. So we should have a period of pi, and zeroes at pi/3, pi
The last graph is your answer.