Answer:
The equation is y =
 x + 4
x + 4
Explanation:
The slope-intercept form of the linear equation is y = m x + b, where
- m is the slope of the line
The rule of the slope of a line is
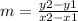 , where
, where
- (x1, y1) and (x2, y2) are two points lie on the line
To find the equation that represents the given table choose two ordered pairs from it
∵ Points (4, 6) and (6, 7) are from the table
∴ x1 = 4 and y1 = 6
∴ x2 = 6 and y2 = 7
→ Substitute them in the rule of the slope to find it
∵
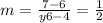
∴ m =

→ Substitute it in the form of the equation above
∴ y =
 x + b
x + b
→ To find b substitute x and y in the equation by the coordinates
of any points from the table
∵ x = 4 and y = 6
∴ 6 =
 (4) + b
(4) + b
∴ 6 = 2 + b
→ Subtract 2 from both sides
∴ 6 - 2 = 2 - 2 + b
∴ 4 = b
→ Substitute its value in the equation above
∴ y =
 x + 4
x + 4
∴ The equation is y =
 x + 4
x + 4